Currently Empty: 0.00 лв.
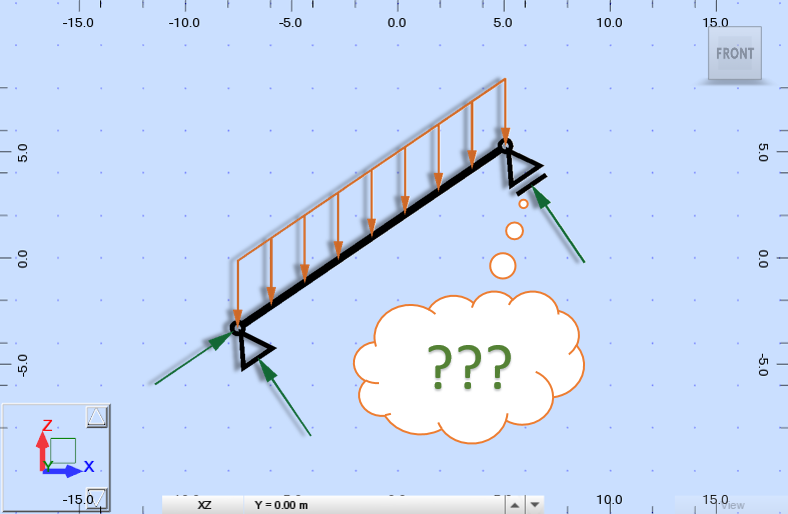
Понякога при моделиране на конструкцията в Robot Structural Analysis се налага използването на наклонена опора, която е завъртяна, така че да не е успоредна на осите на глобалната координатна система. Как това може да стане, след като възлите в Robot ( за разлика от прътите и плочите) нямат локална координатна система?
Изчислителен модел на опорите в Robot Structural Analysis
След като не може да се използва завъртането на локална координатна система на възела, в Robot е предвидена възможност за завъртане на самите опорни условия. Опорите в Robot не са елементи, които поставяме в конструкцията, а са ограничения на преместванията, които прилагаме върху възлите:

За да получим правилни диаграми на усилията в гредата от горната схема е необходимо да завъртим само подвижната опора. Ако искаме обаче да получим и реакциите в локална координатна система, ще трябва да завъртим и неподвижната опора. В следващият пример в Robot са завъртени и двете опори.
Дефиниране на наклона
Завъртането на опората става при дефинирането – избира се бутона Direction и в панела се задава съответният ъгъл. Ако завъртането не е под точен ъгъл, може да изберем възел или точка от пространството, спрямо които да се завърти опората.
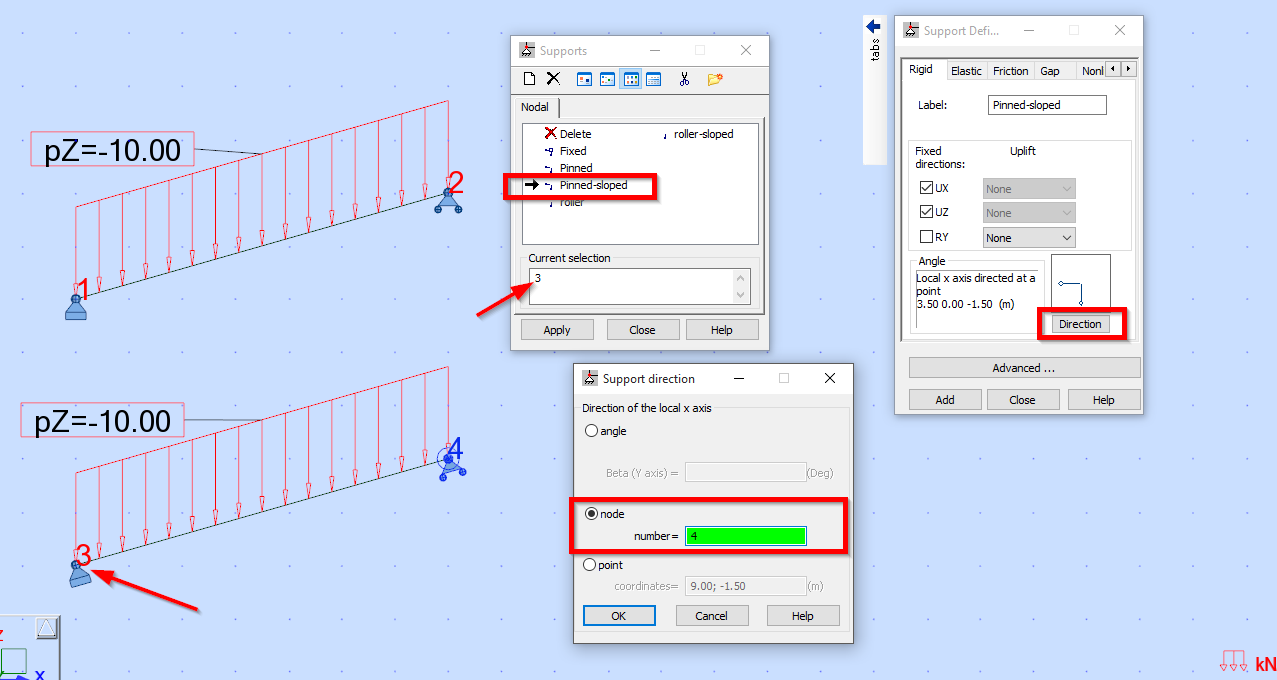
Дефиниции на опори обикновено се прехвърлят в новите модели на Robot автоматично, така че, ако моделирате наклонена опора, запишете това в името й, за да не допуснете грешка с прилагането й на неправилно място в следващи модели.
Разлики в диаграмите
Ето как изглежда диаграмата на осовите усилия при греда с вертикални опори и при наклонени опори:

Ако искате да видите реакциите на наклонените опори в локалната координатна система (в завъртяно положение) то трябва да сложите отметката Reactions in local system:




